
In our example we designed the situation so that regardless of the sensor size, the total light energy deposited on the sensor remained constant. But taking a 200mm f/4 lens, keeping the absolute aperture size the same, and producing a 50mm f/1 lens is incredibly difficult.Īnother concern is that even if the lens is perfect, it can be difficult for a small sensor to accept a high density of photos. To put it in another way, if a 50mm f/4 lens is designed for a 4× crop sensor, then a 200mm f/4 lens can for a full-frame sensor can be produced by simply scaling up the design without internal changes. The main one is that small f-numbers (in other words, the aperture size approaching or exceeding the focal length) become increasingly hard to manufacture - they are expensive and require extensive optical elements to correct for aberrations. In practice however, there are some problems with using small sensor formats. In our example, if both the full-frame and APS-C sensors have the same number of pixels, then each pixel will receive the same amount of light - 64mm f/2.0 full-frame vs. And assuming no losses in the optics, all of that light gets deposited on the smaller sensor. But again, the rate of light gathered by the lens is controlled by the 32mm physical opening of the aperture. The horizontal field of view is still 31.4° because of the new shorter focal length we selected. Now suppose we have a 1.6× crop APS-C sensor and a 37.5mm lens with a 32mm absolute aperture. Assuming an ideal lens with perfect transmission, all of the light is deposited on the sensor. It doesn't matter what components or sensor is behind the lens. The rate of light gathered by the lens (per unit of time) is dictated by the diameter of the absolute aperture. Suppose we have a full-frame sensor and a 64mm lens with a 32mm absolute aperture. Spoiler: It turns out that if you have two sensors of different sizes, and two lenses that have the same absolute aperture but different focal lengths to produce the same angle of view on its respective sensor, then the resulting image will be the same in every way.

The lens is labeled as f/1.667, which makes sense because if we substitute the focal length of 50mm as f, then f/1.667 = 50mm ÷ 1.667 = 30mm, which is precisely the size of the absolute aperture.

For example, a 50mm lens with a 30mm aperture has an f-number of 50÷30 = 1.667.
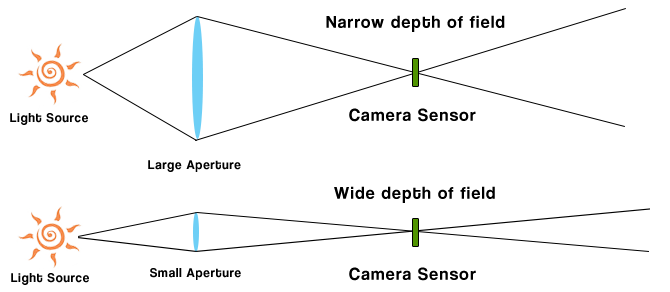
The relative aperture size, or f-number, is defined as the focal length of the lens divided by the absolute aperture size. The absolute aperture size of a lens is the diameter of the opening in the lens's diaphragm - for example 30mm. In theory, both options are equivalent in every way - the low-light performance, the amount of background blur, the angle of view, and everything else.įirst, let's clarify what we mean by aperture size. Ould it be better to have a larger sensor with smaller f-number or a smaller sensor with larger f-number?


 0 kommentar(er)
0 kommentar(er)
